2Bac. Static games

  Content:

Prisoner’s dilemma • Dominant/dominated strategies • Iterated elimination of dominated strategies • Nash equilibrium • Backward induction • Normal and extensive form games • Sub-game perfect equilibrium. 

Anticipating rivals’ moves

 In strategic analysis, it seems important to be able to figure out what one’s rival is going to do, that is, to anticipate a rival’s moves. How can we do this? Strategists (both professional ones (i.e. managers and consultants) and ‘strategists in the making’ (i.e. students)) often assign probabilities to the different actions a rival might take. But can we do better than this? Game theory tells us we can (most of the time)! Let us use an example to illustrate this.

Prisoner’s dilemma – Advertising wars

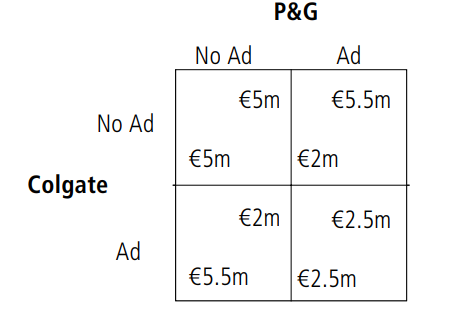
Consider the following situation. P&G and Colgate Palmolive sell competing brands of toothpaste – Crest and Colgate – in a market. The brands share the market equally, that is, both firms have a 50 per cent market share. The overall market for toothpaste is fixed – let’s assume total sales for toothpaste will be €10m per year. Both firms now have the option of launching an advertising campaign for one year at a cost of €2.5m. While advertising does not increase total sales for toothpaste, advertising if the other firm does not advertise would increase market share to 80 per cent. What should both firms do? In fact, can we use the information above to make a prediction of what each of the players is going to do? The first step to take is identifying the players (which is typically a simple but nonetheless important step). In this case, P&G and Colgate Palmolive are the players. The second step is to identify their strategies, that is, what are the choices they have? Here, P&G and Colgate Palmolive decide whether to run an advertising campaign or not. Third, we have to specify the rules of the game. We will go into this in more detail later on, but here the rules are that both players have to decide simultaneously to run or not to run an advertising campaign. Finally, we have to specify the pay-offs for each of the possible outcomes of the game. In this case, both firms not running an ad campaign results in them sharing the market and making sales of €5m. If one of them runs an advertising campaign and the other does not, the first makes sales of €8m (80 per cent of €10m), but has to pay advertising costs of €2.5m, leaving net sales of €5.5m. The other (non-advertising) firm makes sales of €2m. If both firms advertise, their sales will be €5m again (as the market for toothpaste is fixed), but they again incur an advertising cost of €2.5m, resulting in net sales of €2.5m.

We can now represent the game in matrix, or normal form. First, however, a word on convention: The first pay-off (or the leftmost) will be the pay-off of the row player – that is, the player choosing the row (top or bottom), Colgate in this case. The second pay-off (or the pay-off further to the right) will be the column player’s pay-off (i.e. P&G).

 Advertising wars.

The situation P&G and Colgate are facing is what game theorists call a prisoner’s dilemma: overall profits would be higher if both did not advertise, but both have an individual incentive to go ahead and advertise anyway – regardless of what the other player does (advertise or not advertise). This makes advertising a dominant strategy – a strategy that does better than all others for any strategy chosen by the other player(s). This gives us the first way of predicting our rival’s behaviour: if a strategy always maximises my rival’s pay-offs, he will play it.

Eliminating dominated strategies – pizza wars

It would be nice if we could always make a clear prediction about our rival’s behaviour. We can often simplify games by finding dominant strategies as demonstrated above. However, consider the following game. There are two restaurants in a small town, Dave’s Deep Dish and Paul’s Pizza Pies. They are in competition with each other for customers and can choose their prices: high (H), medium (M) or low (L). The city has 1,000 customers, of which 300 only ever buy at Dave’s, and 300 only buy at Paul’s. The other 400 are price-sensitive and always buy the cheaper pizza and choose at random if they charge the same price. Both places make a margin of £12 per pizza if they charge high prices, £10 per pizza if they charge medium prices, and £5 for low prices. Both Dave and Paul cannot observe what the other player has chosen before they choose themselves. Can we draw this in a pay-off matrix? We know players, strategies and rules. What about calculating pay-offs? We can calculate profits by multiplying the number of customers with the margin per customer. For example, if Dave charges a medium price and Paul a high price, Dave will sell to his 300 ‘loyal’ customers and the 400 ‘price sensitive’ customers at a margin of £10 each, giving him pay-offs of £7,000. Paul only sells to his 300 loyal customers, but at a margin of £12 per pizza, giving him profits of £3,600

Pizza wars. 

Can we solve this game by finding dominant strategies? For none of the players can we find one strategy that does better than the other two for all strategies chosen by the rival. For example, M outperforms H if the other price is H or M, but not if it if L. Dominant strategies will not get us very far then. We can, however, find a strategy that never does better than another one – a dominated strategy: charging L is worse than H or M for all strategies chosen by the other player. So if Dave and Paul are (as we assume) trying to maximise their profits, they will never charge lower prices. We combine our outcomes on dominant and dominated strategies for the following set of predictions. 

Result 

. A dominant strategy should always be played.

A dominated strategy will never be played